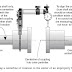
An agitated tank is often used as an example of a first-order lag process. However, mixing in real tanks falls far short of the ideal well-mixed tank. Real tanks have composition responses that are a combination of a first-order lag and deadtime. If the pumping rate of the agitator (Fa) is known, the deadtime (Td) of the real tank may be estimated by the following equation: Td = V/(F+Fa), where V is the volume of the tank and F is the flow through it.
Process responses often consist of multiple lags in series. When these lags are non-interacting, the resulting response is predominantly deadtime, varying linearly with the number of lags in series. However when these lags are interacting, such as the trays on a distillation column, the resulting response remains predominantly a first-order lag with a time constant proportional to the number of lags squared.
Other process characteristics that affect control performance are both steady-state and dynamic non-linear behavior. Steady-state non-linear behavior refers to the steady-state gain varying, dependent upon operating point or time. For example, the pH of a process stream is highly non-linear, dependent upon the operating point on the titration curve. Further, depending upon the stream component composition, the titration curve itself may vary over time.
Non-linear dynamic behavior can occur due to operating point, direction, or magnitude of process changes. For example, the time constant of the composition response for a tank will depend upon the operating point of liquid level in the tank. Some processes will respond in one direction faster than in the other direction, particularly
as the control valve closes. For example, liquid in a tank may drain quite rapidly, but once the drain valve closes the level can only rise as fast as the inlet stream flow allows. The magnitude of a change may cause different dynamic response whenever inherent response limits are reached. Process examples may include a transition
to critical flow, or a transition from a heat transfer to a mass transfer limiting mechanism in a drying processes.
These non-linearities are the main reason an operating margin must be considered when tuning the controller. If the loop is to be robust and operate in a stable manner over a wide range of conditions, conservative values of the tuning parameters must be chosen. Unfortunately, this results in poorer performance under most conditions. One technique to handle known non-linearities is to provide tuning parameters that vary based upon measured process conditions.